D-H参数法

(14条消息) 一文带你完全掌握机器人DH参数建模(详细步骤+实例+代码)_Marc Pony的博客-CSDN博客_dh建模

坐标变换矩阵

(14条消息) 详解坐标变换矩阵_Akinaze的博客-CSDN博客_坐标变换矩阵

D-H参数

​ 一般来说，想要得到两个坐标系之间的变换矩阵，需要知道六个量。但是在使用D-H参数法时，需要按照特定方式建立坐标系，依托于这些“前提约束”，我们只需要4个参数便可以得出两坐标系之间的变换矩阵。

先要理解坐标系的建立规定

  • z轴的方向垂直于旋转面，即为转轴;

  • x[i]方向的确定：同时垂直于z[i]与z[i-1];

依据这样的规定，可以发现：

  • z[i-1]同时垂直于x[i-1]与x[i];

  • x[i]同时垂直于z[i-1]与z[i];

由此，z[i-1]和x[i]便成了连接坐标系[i-1]和坐标系[i]的重要参考。再看四个参数的定义

  • d[i]:坐标轴x[i-1]与坐标轴x[i]沿着z[i-1]的有向距离；
  • θ[i]:坐标轴x[i-1]与坐标轴x[i]以z[i-1]为转轴的旋转角(逆时针，xi在前为正，或者说从x0转到x1的角度)；
  • a[i]:坐标轴z[i-1]与坐标轴z[i]沿着x[i]的有向距离；
  • α[i]:坐标轴z[i-1]与坐标轴z[i]以x[i]为转轴的旋转角；

正向求解

在已知各关节角度的条件下，求出机械臂末端的坐标。

由D-H参数可以得到坐标系变换矩阵（将其记作$T_i$）：

​ 代入i系的点$(x_i,y_i,z_i)$，左乘变换矩阵$T_i$，得到这个点在i-1系的坐标。由此，将末端坐标$C_n$不断左乘各变换矩阵，便可以递推出其在第一个坐标系的坐标$C_0$。

代码实现

主要就是两个部分

  • 矩阵Matrix的构建及其运算
  • 机械臂robotic_arm的构建及基本功能

​ 都是直接模拟手算过程，矩阵相乘的时间复杂度是O(mnk)，三次方量级的，好在矩阵规模都比较小。

结构体

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
/**
 * @brief 
 * 
 */
typedef struct __Matrix_t{
    int m;
    int n;
    double matrix[Matrix_MX][Matrix_MX];
}Matrix_t;

/**
 * @brief 
 * @param
 */
typedef struct __robotic_arm_t{
    int n;//number of nodes
    float d[arm_MX_nodes],a[arm_MX_nodes];
    double theta[arm_MX_nodes],alpha[arm_MX_nodes];
    Matrix_t *T[arm_MX_nodes];

}robotic_arm_t;

机械臂初始化

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
/**
 * @brief 
 * @param n the number of the nodes
 * @param d D-H parameters
 * @param a D-H parameters
 * @param theta D-H parameters
 * @param alpha D-H parameters
 * @return robotic_arm_t* 
 */
robotic_arm_t *robotic_arm_init(int n, float *d, float *a, double *theta, double *alpha)
{
    robotic_arm_t *arm;
    arm = (robotic_arm_t*)malloc(sizeof(robotic_arm_t));
    for(int i=1;i<=n;i++)
    arm->T[i] = (Matrix_t*)malloc(sizeof(Matrix_t));

    arm->n = n;
    for(int i=1;i<=n;i++)
    {
        arm->d[i] = d[i];
        arm->a[i] = a[i];
        arm->alpha[i] = alpha[i];
        arm->theta[i] = theta[i];
    }

    get_Trans(arm);

    return arm;
}

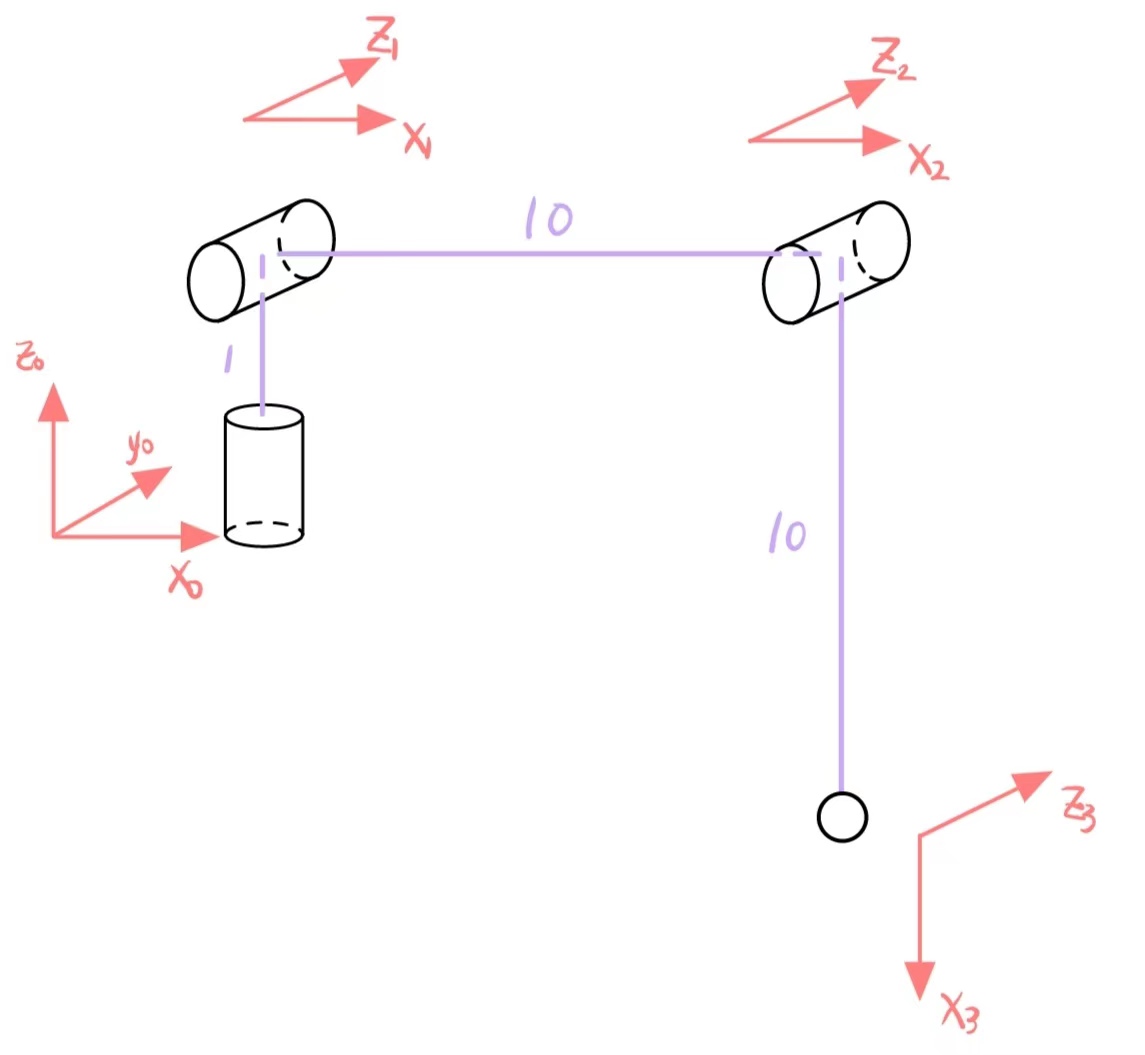
我这里构建的模型

robotic_arm.jpg

0 1 2 3
d 0 1 0 0
θ 0 $\omega_0$ -$\omega_1$ $\frac{\Pi}{2} - \omega_2$
α 0 $-\frac{\Pi}{2}$ 0 0
a 0 0 10 10 
1
2
3
float test_d[4]={0,1,0,0},test_a[4]={0,0,10,10};
double test_theta[4]={0},test_alpha[4]={0,-PI/2,0,0};
test_arm = robotic_arm_init(3,test_d,test_a,test_theta,test_alpha);

$\omega$为关节（舵机）角度，以图中状态作为初始值，认为此时关节（舵机）角度为0。所以还有一个由关节角度到DH参数的转换函数，这个函数就是根据机械臂具体情况具体修改了。

1
2
3
4
5
6
7
8
void DH_update(robotic_arm_t *arm, double *servo)
{
    arm->theta[1] =  servo[0];
    arm->theta[2] = -servo[1];
    arm->theta[3] =  PI/2-servo[2];
    get_Trans(arm);
    return;
}

计算转移矩阵T

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
/**
 * @brief Get the Transparent Matrix relay on the current arm state
 * @param arm 
 */
void get_Trans(robotic_arm_t *arm)
{
    for(int i=1; i<=arm->n; i++)
    {
        arm->T[i]->m=4, arm->T[i]->n=4;
        arm->T[i]->matrix[0][0] =  cos(arm->theta[i]);
        arm->T[i]->matrix[0][1] = -sin(arm->theta[i])*cos(arm->alpha[i]);
        arm->T[i]->matrix[0][2] =  sin(arm->theta[i])*sin(arm->alpha[i]);
        arm->T[i]->matrix[0][3] =  arm->a[i]*cos(arm->theta[i]);

        arm->T[i]->matrix[1][0] =  sin(arm->theta[i]);
        arm->T[i]->matrix[1][1] =  cos(arm->theta[i])*cos(arm->alpha[i]);
        arm->T[i]->matrix[1][2] = -cos(arm->theta[i])*sin(arm->alpha[i]);
        arm->T[i]->matrix[1][3] =  arm->a[i]*sin(arm->theta[i]);

        arm->T[i]->matrix[2][0] =  0;
        arm->T[i]->matrix[2][1] =  sin(arm->alpha[i]);
        arm->T[i]->matrix[2][2] =  cos(arm->alpha[i]);
        arm->T[i]->matrix[2][3] =  arm->d[i];

        arm->T[i]->matrix[3][0] =  0;
        arm->T[i]->matrix[3][1] =  0;
        arm->T[i]->matrix[3][2] =  0;
        arm->T[i]->matrix[3][3] =  1;
    }
    return;
}

正向求解

1
2
3
4
5
6
7
8
9
10
11
12
13
/**
 * @brief Get the coordinates of the point in the end coordinate system in the main coordinate system
 *        Suppose the main coordinate system's number is 0
 *        得到末端坐标系中的一个点在主坐标系中的坐标,假设主坐标系编号为0
 * @param arm 
 * @param point 
 */
void foward_solve(robotic_arm_t *arm, Matrix_t *point)
{
    for(int i=arm->n; i>0; i--)
    *point = multiply_matrix2(arm->T[i],point);
    return;
}

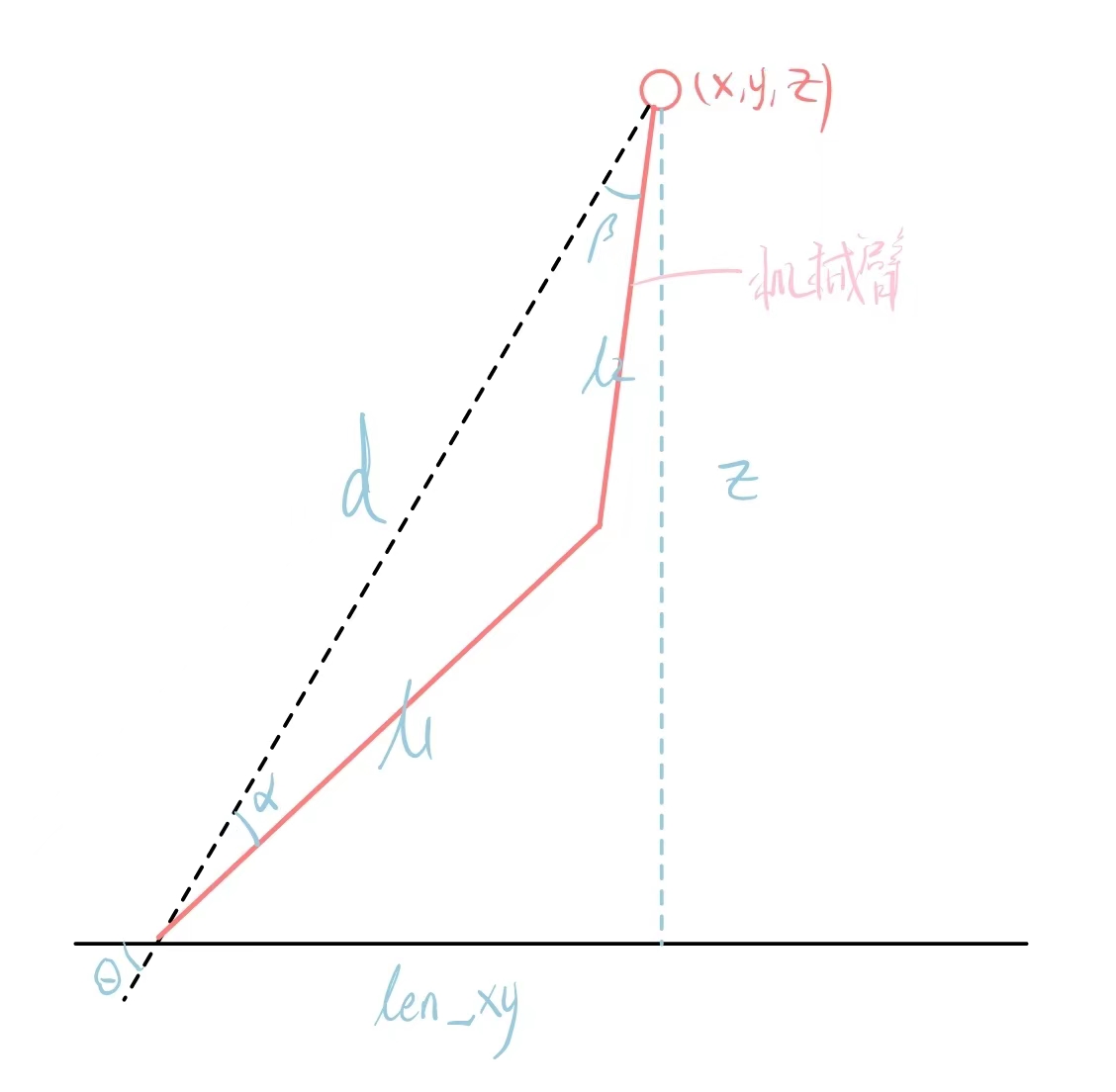
逆向求解

​ 针对于我手上的机械臂，直接采用几何法分析。可是方程我解不出来😂，于是将其稍微变形，利用二分法也能迅速求得符合精度要求的解。

几何逆解.jpg

具体二分的思路就是alpha越大，机械臂伸得越短，alpha越小，伸得越长。比较伸的长短是否到达

代码实现

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
/**
 * @brief Use the dichotomy method to find the angle of each joint according to the target coordinates 
 *        用二分法根据目标坐标求出关节角度。（使用了几何法，仅适用于特定机械臂）
 *        根据末端机械手位姿求出最后一个关节的坐标(这一步还没实现)，由此计算其余关节角度。
 * @param arm 自己的机械臂，非通解
 * @param point 最后一个关节的坐标
 */
void reverse_solve_dichonomy(robotic_arm_t *arm, Matrix_t point)
{
    double angle0, angle1, angle2, alpha_l=0, alpha_r=PI, alpha_mid, beta, theta, len_xy, x, y, z, l1, l2, d;
    x = point.matrix[0][0], y = point.matrix[1][0], z = point.matrix[2][0] - arm->d[1];
    d = sqrt(x*x + y*y + z*z);
    l1 = arm->a[2], l2 = arm->a[3];
    len_xy = sqrt(x*x + y*y);
    if(len_xy == 0) {theta = PI/2;}
    else {theta = atan(z/len_xy);}

    while(alpha_r-alpha_l > 0.00175)
    {
        alpha_mid = (alpha_l+alpha_r)/2;
        beta = asin(sin(alpha_mid)*l1/l2);
        if(l1*cos(alpha_mid) + l2*cos(beta) > d)
        {alpha_l = alpha_mid;}
        else 
        {alpha_r = alpha_mid;}
    }
    if(x == 0) {angle0 = PI/2;}
    else {angle0 = atan(y/x);}
    angle1 = theta - alpha_mid;
    angle2 = alpha_mid + beta + PI/2;
    arm->theta[1] =  angle0;
    arm->theta[2] = -angle1;
    arm->theta[3] = PI/2 - angle2;

    return;
}

我也尝试了使用MATLAB解方程，得出的结果十分的复杂，我觉得还是直接用二分法比较好。

MATLAB.png

粒子群优化算法

​ 在之前的逆解过程中，只能针对单个机械臂的几何特征单独求解，不具有泛用性。而且以我的数学水平也只能求解结构简单的机械臂🤣，当关节数增加甚至冗余时，无法直接用数学方法求解，或者说是多解。所以尝试采用粒子群优化算法(Particle Swarm Optimization, PSO)来实现一种通用的解法。

粒子群优化算法(Particle Swarm Optimization, PSO)的详细解读 - 知乎 (zhihu.com)

这位大佬写得非常详细，我这里是使用c语言实现的，并将其用在了机械臂逆解上面。

代码实现

基本流程

  • 粒子群初始化及各粒子随机初始化
  • 开始迭代
    • 计算适应值
    • 更新个体及群体最优解与最优适应值
    • 更新w值，粒子速度，粒子位置
  • 结束迭代
  • 返回寻得的最优解

结构体

看完上面的博客之后，想必这些定义是很容易理解的

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
/**
 * @brief 
 * @param X current state 目前坐标（解）
 * @param V current velocity 目前速度
 * @param opt_X optimal solution of individual's history 个体历史最优解
 * @param opt_A optimal adaptability of individual's history 个体历史最优适应值
 */
typedef struct __bird_t{
    double X[arm_MX_nodes], V[arm_MX_nodes];
    double opt_X[arm_MX_nodes];
    double opt_A;
}bird_t;

/**
 * @brief 
 * @param N size of the bird population 种群规模
 * @param D 解的维度
 * @param K 迭代次数
 * @param W 惯性权重
 * @param C_ind 个体学习因子
 * @param C_pop 群体学习因子
 * @param opt_X_pop optimal solution of population's history 群体历史最优解
 * @param opt_A_pop optimal adapatability of population's history 群体历史最优解
 */
typedef struct __bird_population_t{
    int N, D, K;
    double W, C_ind, C_pop;
    double opt_X_pop[arm_MX_nodes];
    double opt_A_pop;
    bird_t *bird[N_MX_SIZE];

}bird_population_t;

初始化

​ 单个粒子的初始化，至于为什么要用 ‘bird’ 来命名呢，因为这个算法其实也算是一种仿生的思路，作者是受到鸟群觅食的启发发明了这个算法。我第一眼看到这个算法想到的就是遗传算法，其实感觉都是优化的搜索方法，不过相比于遗传算法此算法在求机械臂逆解的应用中更胜一筹，具体怎么个优势法还有待去研究研究。

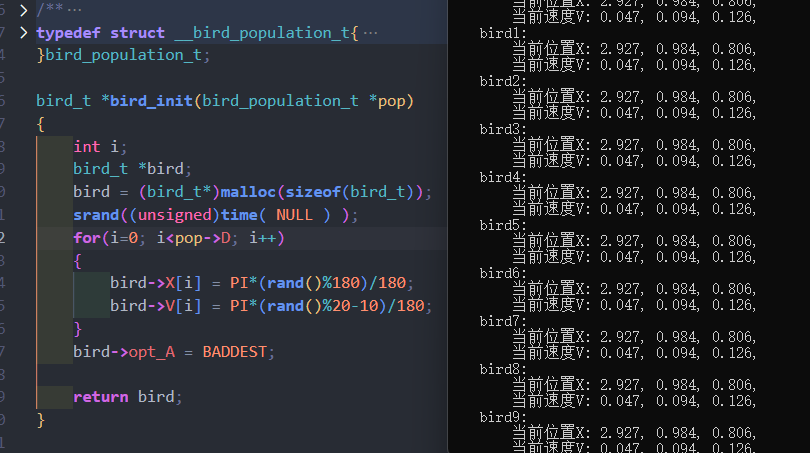
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
/**
 * @brief 粒子随机初始化
 * 在这里面分配空间一定程度上也可以防止空间浪费
 * @param pop 
 * @return bird_t* 
 */
bird_t *bird_init(bird_population_t *pop)
{
    int i;
    bird_t *bird;
    bird = (bird_t*)malloc(sizeof(bird_t));
    for(i=0; i<pop->D; i++)
    {
        bird->X[i] = PI*(rand()%180)/180;
        bird->V[i] = PI*(rand()%20-10)/180;
    }
    bird->opt_A = BADDEST;

    return bird;
}

/**
 * @brief 粒子群初始化
 * @param n 
 * @param d 
 * @param k 
 * @param w 
 * @param c_ind 
 * @param c_pop 
 * @return bird_population_t* 
 */
bird_population_t *bird_population_init(int n, int d, int k, double w, double c_ind, double c_pop)
{
    bird_population_t *bird_population;
    bird_population = (bird_population_t*)malloc(sizeof(bird_population_t));

    bird_population->N = n, bird_population->D = d, bird_population->K = k;
    bird_population->W = w, bird_population->C_ind = c_ind, bird_population->C_pop = c_pop;

    srand((unsigned)time( NULL ) );     
    for(int i=0; i<n; i++)
    {
        bird_population->bird[i] = bird_init(bird_population);
    }
    bird_population->opt_A_pop = BADDEST;
    return bird_population;
}

迭代过程

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
for(i=0; i<bird_pop->K; i++)//K
    {
        for(j=0;j<bird_pop->N;j++)//N
        {
            //计算适应值
            Matrix_t *judge_point = point_init(0,0,0);
            double ada=0;//适应值
            DH_update(arm,bird_pop->bird[j]->X);
            foward_solve(arm,judge_point);
            ada += (point.matrix[0][0] - judge_point->matrix[0][0])*(point.matrix[0][0] - judge_point->matrix[0][0]);
            ada += (point.matrix[1][0] - judge_point->matrix[1][0])*(point.matrix[1][0] - judge_point->matrix[1][0]);
            ada += (point.matrix[2][0] - judge_point->matrix[2][0])*(point.matrix[2][0] - judge_point->matrix[2][0]);
            
            //更新个体与群体最优适应值与最优解
            if(ada < bird_pop->bird[j]->opt_A)
            {
                bird_pop->bird[j]->opt_A = ada;
                for(k=0; k < arm->n; k++)
                {bird_pop->bird[j]->opt_X[k] = bird_pop->bird[j]->X[k];}
            }
            if(ada < bird_pop->opt_A_pop)
            {
                bird_pop->opt_A_pop = ada;
                for(k=0; k < arm->n; k++)
                {bird_pop->opt_X_pop[k] = bird_pop->bird[j]->X[k];}
            }
            
            //更新w值，更新各维度速度与位置
            w = W_MAX - (W_MAX - W_MIN)*((double)i/bird_pop->K);
            for(k=0; k < arm->n; k++)
            {
                bird_pop->bird[j]->V[k] = (w+(rand()/16384-1)*0.15)*(bird_pop->bird[j]->V[k]) + (rand()/16384)*1.8*(bird_pop->opt_X_pop[k] - bird_pop->bird[j]->X[k]) + (rand()/16384)*1.6*(bird_pop->bird[j]->opt_X[k] - bird_pop->bird[j]->X[k]);
                bird_pop->bird[j]->V[k] = (bird_pop->bird[j]->V[k] > V_MAX) ? V_MAX : bird_pop->bird[j]->V[k];
                bird_pop->bird[j]->V[k] = (bird_pop->bird[j]->V[k] < V_MIN) ? V_MIN : bird_pop->bird[j]->V[k];
                bird_pop->bird[j]->X[k] += bird_pop->bird[j]->V[k]; 
                bird_pop->bird[j]->X[k] = (bird_pop->bird[j]->X[k] > X_MAX) ? X_MAX : bird_pop->bird[j]->X[k];
                bird_pop->bird[j]->X[k] = (bird_pop->bird[j]->X[k] < X_MIN) ? X_MIN : bird_pop->bird[j]->X[k];
            }
            
            //打印调试
            printf("    bird%d: \r\n        当前位置X: ",j);
            for(int m=0; m<arm->n; m++) {printf("%.3f|%.1f, ",bird_pop->bird[j]->X[m],rad_angle(bird_pop->bird[j]->X[m]));}
            printf("\r\n        当前速度V: ");
            for(int m=0; m<arm->n; m++) {printf("%.3f|%.1f, ",bird_pop->bird[j]->V[m],rad_angle(bird_pop->bird[j]->V[m]));}
            printf("\r\n");
            free(judge_point);
        }
    //打印调试
    printf("%d 最适值: %.3f 惯性w: %.3f\r\n",i,bird_pop->opt_A_pop,w);
    printf("   角度X: ");
    for(k=0; k < arm->n; k++) {printf("%.2f|%.1f ",bird_pop->opt_X_pop[k],rad_angle(bird_pop->opt_X_pop[k]));}
    printf("\r\n");

    }

一些小细节

bug1.png

​ 可以看到，虽然我添加了时间随机数种子，但是生成的粒子仍然是全都一样的。这里要将srand((insigned)time(NULL));提前至初始化函数外。

​

w = W_MAX - (W_MAX - W_MIN)*((double)i/bird_pop->K); 在给w加权的时候别忘了double，不然后面算出来一直是0。

写在最后

感谢大家耐心看完了本篇博客，如果觉得不错的话欢迎分享给他人。由于本人水平有限，难免有错误的地方，也欢迎在评论区批评指正。完整的代码可以在我的代码仓库找到，后续也会将其移植到STM32上。在这里贴上主要代码方便随时查看，思路与代码相互对照也更容易理解。