PID波形绘制及积分优化
MATLAB串口绘制波形
对于MATLAB我也是久仰大名,最近安装了一个,感觉功能很丰富,也比较有意思。当然本人也是刚安装MABLAB不久,对其理解还是分浅薄,暂时也只是一些简单的使用。
函数说明
plot( ) 二维绘图
二维线图 - MATLAB plot - MathWorks 中国
axis( ) 显示范围
(15条消息) Matlab axis函数_Geek猫的博客-CSDN博客_matlab axis
grid 栅格
Display or hide axes grid lines - MATLAB grid (mathworks.com)
代码实现
新建函数文件——Serial.m
1 | function Serial() %创建函数 |
另建回调函数文件Callback.m
1 | function Callback(obj,event) %创建中断服务函数,绘制图像 |
样式预览
可以参考下文。
积分优化
梯形积分PID
从微积分的角度来说,当微分到无限小时,矩形积分与梯形积分是没有区别的。但是实际上采样时间不可能无穷小,采样周期越大,偏差就越大。而梯形积分则是更加接近实际曲线,所以用梯形积分可以得到更高的精度。
积分分离PID
在普通的PID控制算法中,由于积分系数是常数,所以在整个控制过程中,积分增量不变。而系统对积分项的要求是:
在普通的PID控制算法中,引入积分环节目的主要是为了消除静差。
基本思想
思路是偏差值较大时,取消积分作用,以免超调量增大;而偏差值较小时,引入积分作用,以便消除静差,提⾼控制精度。
具体的实现步骤是:根据实际情况,设定⼀个阈值
- 当偏差大于阈值时,消除积分仅用PD控制;
- 当偏差小于等于阈值时,引⼊积分采⽤PID控制。
积分项表达式
其中β称为积分开关系数
由上述表述及公式我们可以知道,积分分离算法的效果其实与ε值的选取有很大的关系,所以ε值的选取是实现的难点
ε值过大则达不到积分分离的效果
ε值过小则难以进入积分区。
变速积分PID
基本思想
变速积分PID的基本思想是
- 偏差越大,积分越慢;
- 偏差越小则越快。
为此,设置系数f(e(k)) ,它是e(k)的函数。当e(k)增大时, f减小,反之增大。
积分项表达式
f(e(k))可根据具体情况设定,比较简单的设置为:
由上述公式可知,f(e(k))的值在[0,1]区间变化。
当偏差值e(k)大于分离区间A + B时,不对当前e(k)进行累加;
当偏差值e(k)小于B时,加入当前偏差e(k)进行累加;
介于B和A + B之间时,按一定函数关系变化。
这种算法对A,B两个参数的要求不精确,参数整定较容易。
代码示例
1 | typedef struct __PID_t{ |
虽然定义的是I_up,I_low, 但是实际上这是与error相比较的
效果展示
Kp = 350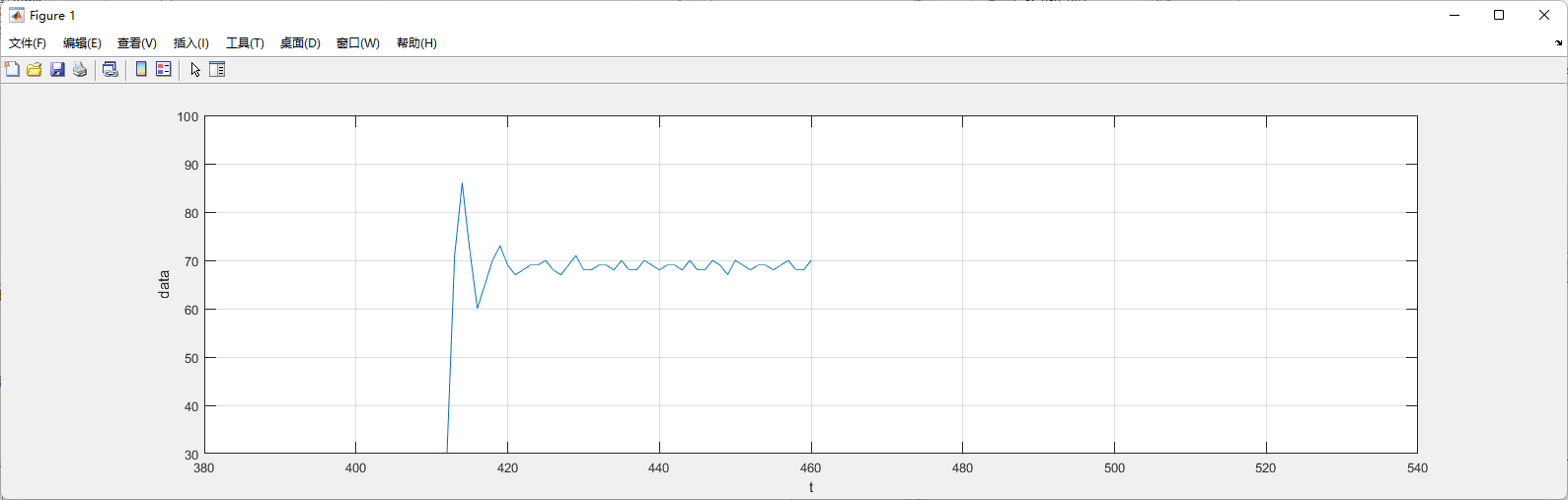
ki = 120
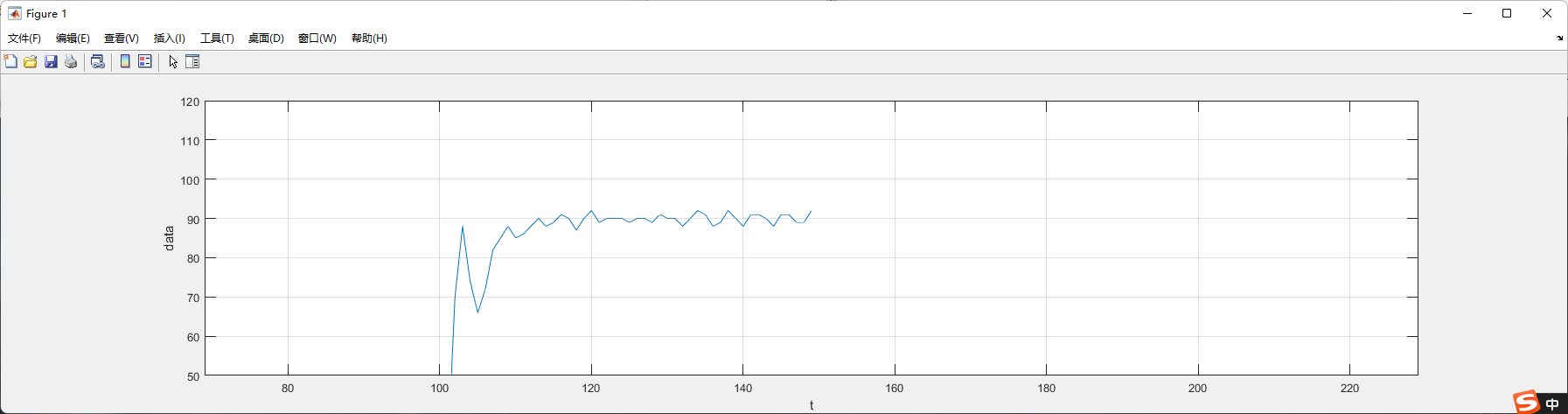
Kd = 100
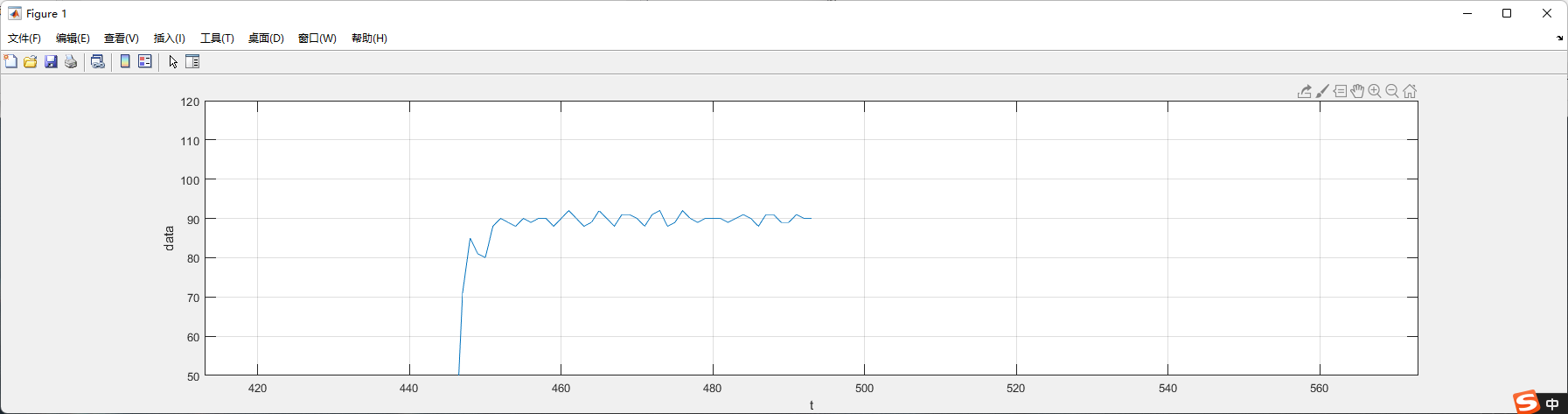
Kd = 80, up = 80, low = 50